Cryptography I - Stanford University - Week 1
Nov 24, 2019CryptographyStream Cipher Share on:
Week 1. This week’s topic is an overview of what cryptography is about as well as our first example ciphers. You will learn about pseudo-randomness and how to use it for encryption. We will also look at a few basic definitions of secure encryption.
History
Symmetric ciphers: - substitution ciphers (breaking by entropy attack) - Caesar cipher (bad substitution cipher because no key (if you know the number of shifts, you win)) - Vigener cipher (have a key that’s concatenated as long as there is plaintext, then take CipherText = (key + plaintext mod 26)). When we discover the key size, we can thus perform an entropy attack on every letter. - Rotor Motor : - Hebern: Rotor-powered substitution table -> statistical attacks - Enigma (2^18 keyspace) - broken by cipher text attacks
- DES (1974, NIST standard)
- 2^56 keyspace -> can be bruteforced these days, not to be used anymore
- blocks size 64 bits
Now: AES, SALSA20
Discrete Probability
Not much new material covered => See chapter in DS course for more info.
Random variable, events, independence, XOR …
XOR has the amazing property of always adding entropy, never removing it.
Birthday paradox
when n = 1.2 x U^(1/2) ==> Pr[there exists two similar elements] >= 1/2
Stream ciphers
Information theoretic security
A cipher is defined over a triple ( the key space, message space, cipher space) and does provide two functions E and D in such a way that D(k, E(k,m)) = m.
E is sometimes randomised but D is always deterministic.
The Vernam Cipher is a cipher where the key is as long as the message where the cipher text is obtained by E(m,k)=(message XOR key) = cipher text and D(c,k) = c XOR k = message.
Vernam is not useful in practise because if we have a secure channel to send the keys over, we could use that to send the message, so what’s the point of the cipher, right?
A cipher (E,D) over (K, M, C) has perfect secrecy if for every m_0 and m_1 in M, length of m_0 is equal to the length of m_1 and for every c in C, Pr[E(k,m_0) = c] = Pr[E(k, m_1)=c].
Perfect secrecy means that there are no cipher text only attack!
If one cipher has perfect secrecy => |K| >= |M|, the key_length >= message_length.
Stream ciphers
Idea: replace random key by pseudorandom key.
For the stream ciphers, we introduce a PRG: Pseudo-random generator.
A PRG is a deterministic function G:{0,1}^s (seed space) -> {0,1}^n, n>>s.
In stream ciphers, seed = key and define the following operations.
E(k,m) := m XOR G(k)
D(k,c) := c XOR G(k)
PRG
A PRG must be unpredictable for a stream cipher to be secure.
We say G:K -> {0,1}^n is predictable if there exists an efficient algorithm A and there exists an i: 1
In short, a PRG is unpredictable: for all i, there is no efficient algorithm A, that can predict the i+1 bit following the prefix.
NEVER USE Weak PRGs: Linear congruential generators (glibc random).
Negligible and non-negligible - In practise, epsilon is a scalar such as the event is not likely to happen. In theory, non-neg is defined as there exists d: epsilon(polynomial lambda) >= 1/(lambda^d) infinitely often.
TLDR’: The function is negligible if it’s less than all polynomial fractions.
Attacks on OTP / stream ciphers
The two time pad is insecure.
Example:
c_1 = m_1 XOR PRG(k)
c_2 = m_2 XOR PRG(k)
If an attacker gets c_1 and c_2, he can perform c_1 XOR c_2 = m_1 XOR m_2
The english language (and ASCII encoding) has enough redundancy to find m_1 and m_2.
Vulnerabilities found in Project Venona (1941-1946), MS-PPTP (Windows NT) and WEB where the same pad would be used every 16M frames. Even worse, most Wi-Fi cards do reset their IV back to zero on restart, causing the two time pad to appear way quicker because IC is concatenated with a long-term identity key.
In disk encryption, issue of the one time pad is malleability. Because OTP does not provide integrity-checking, cipher text could be altered without the user knowing. If you know the difference between two strings, you can XOR that difference on the cipher text without knowing the key and it be changed in the cipher text without you having to know the key.
Modern broken stream ciphers
RC4 (1987) - stream cipher designed to be implemented in software- takes a variable size seed, expands it to a broader number of bits and then generates 1 byte (of pseudorandom) per round. Used in HTTPS and WEP.
- Weaknesses:
- Bias in initial output: ex.
Pr[2nd byte = 0] = 2/256if seed = 128bits and expansion to 2048bits. (256th first bytes are biased) Pr[(0,0)]is getting bigger than it should after a few gigs of data. Should not be used anymore.- Related key attacks
- Bias in initial output: ex.
CSS - Content scrambling system is a stream-cipher used for encrypting DVDs. It’s badly broken. CSS was designed in the 1980’s when exportable encryption was restricted to 40-bit keys. As a result, CSS encrypts movies using a 40-bit secret key. It was designed to be implemented on hardware and based on a mechanism called LFSR (linear feedback shift register), also used for GSM encryption (A5/1,2) and Bluetooth (E0). LFSR-derived stream ciphers are all badly broken but hard to fix because implemented in hardware.
How LFSR works:
- We have a register of n bits.
- At every clock cycle, we shift the entries of the registry to the left, the last bit falls off and the first bit becomes the result of the XOR of all bits of the register of the previous state.
- Seed = initial state of the register.
CSS:
- seed = 5 bytes = 40 bits (because crypto-regulations in the US only allowed exports of crypto using 40 bits keys!)
- 2 LFSRs (17-bit and 25-bits). The first one is seeded with (1 + first 2 bytes of the key) and the second one is seeded with (1 + last 3 bytes of the key). Each of the LFSRs do produce 8 bits outputs (in 8 cycles) that are then added and mod 256 + carry of previous block. And this outputs one byte per round that is then XORed with the byte of the movie we are trying to encrypt.
CSS can be broken in 2^17.
Better modern stream cipher
Better PRG are coming from the eStream project (2008).
PRG: {0,1}^s x R (nonce) -> {0,1}^n
A nonce is a non-repeating value for a given key.
E(k,m,r) = m xor PRG(k,r)
The pair (k,r) is never used more than once => You can reuse the key because a nonce make the key unique.
Let’s do some Salsa!
Salsa20 was designed to be easy to implement on both software and hardware. It was part of the eStream project and was submitted by DJB.
Salsa20: {0,1}^{128 or 256} x {0,1}^64 -> {0,1}^n (max n=2^73)
Salsa20(k,r) := H(k, (r,0) ) || H(k, (r,1) ) || …
How is that function H(k, (r,i) ) defined? k –> seed; r –> nonce; i –> counter
Salsa20 uses 128 and 256 bits keys.
For the 128 version of Salsa20, we start with 64 bytes defined as in this slide. T_0…3 is defined in the Salsa20 specification. You perform 10 rounds of an invertible function h and do add all of the them word by word and you get a 64 byte output.
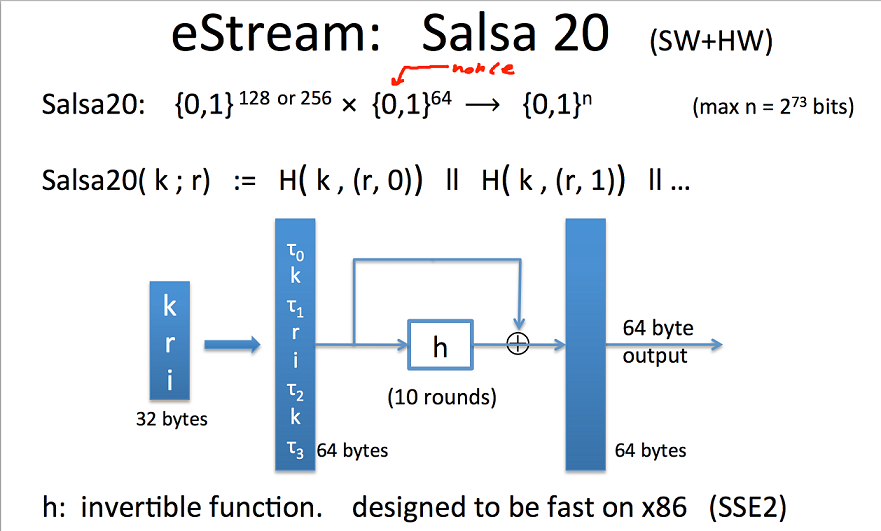
There are no significant attacks known on Salsa20. Very fast stream cipher in both software and hardware. In crypto++, RC4 = 126 MB/s and Salsa20=643 MB/s.
Performance:
| cipher | speed1(MB/sec) |
|---|---|
| RC4 | 126 |
| SEAL | 375 |
| Salsa20 | 408 |
| Sosemanuk | 727 |
PRG Security
The seed space is really small compared to the universe {0,1}^n. A pseudorandom generator outputs would look indistinguishable from a uniform distribution on {0,1}^n.
One way to test if a PRG is pseudorandom we do perform statistical tests.
Statistical Test:
An algorithm that is used to distinguish a pseudo-random string G(s) from a truly random string r is called a statistical test. How do we evaluate if a statistical test is good? We define the advantage of a statistical test A over the generator G:
Adv[A,G] = | Pr[A(G(k))=1 ]- Pr[A(r) =1] | (between 0,1)
If the advantage happen to be close to 1 it means that the generator behaved differently from the random distribution. This statistical test can distinguish the difference from random. If the advantage is close to 0, A can not distinguish the generator from random.
The test A is said to break the generator if it has an advantage close to 1.
If the statistical test always outputs 0, it’s advantage is 0.
We define a secure PRG such as, for all statistical tests A, Adv[A,G] is negligible.
So, can we prove it? No we can’t. ( p != np) but we have heuristic candidates.
If PRG is predictable => PRG is insecure (can be proved easily by using the advantage definition of a secure PRG). If next-bit predictors cannot distinguish G from random then no statistical test can!
What is a secure cipher?
We can adapt the definition of perfect secrecy from Shannon with the concept of computational indistinguishability.
For every message m_0, m1 in M: E(k, m_0) is computationally indistinguishable from E(k, m_1).
A cipher is semantically secure if;
for all efficient adversary A, Adv[A, cipher] is negligible.