Z-r0crypt

Security …

Copyright © 2024 License
Powered by Hugo and Hyde-X

Cryptography I - Week 2 - Part 1

Feb 3, 2020
CryptographyBlock Cipher Share on:
  1. Block Ciphers
  2. Data Encryption Standard
  3. Advanced Encryption Standard (AES) Block Cipher
  4. Building Block Ciphers from PRGs

Block Ciphers

A block cipher maps n bits of inputs to n bits of output. Examples : - 3DES: n=64bits, k=168 bits - AES: n=128bits, k = 128,192,256 bits

Block ciphers are typically built by iteration with a round function R(k, m). It takes as input the round key k and the message m. The key k is expanded into ‘round keys’ k1, k2, … kn. The message m is then encoded using R that stands for round function, which takes one of the round keys, and the current state of the message /mi/. This sequence of steps is applied iteratively until we reach /kn/, and the concatenation of the output of R is our cipher text.

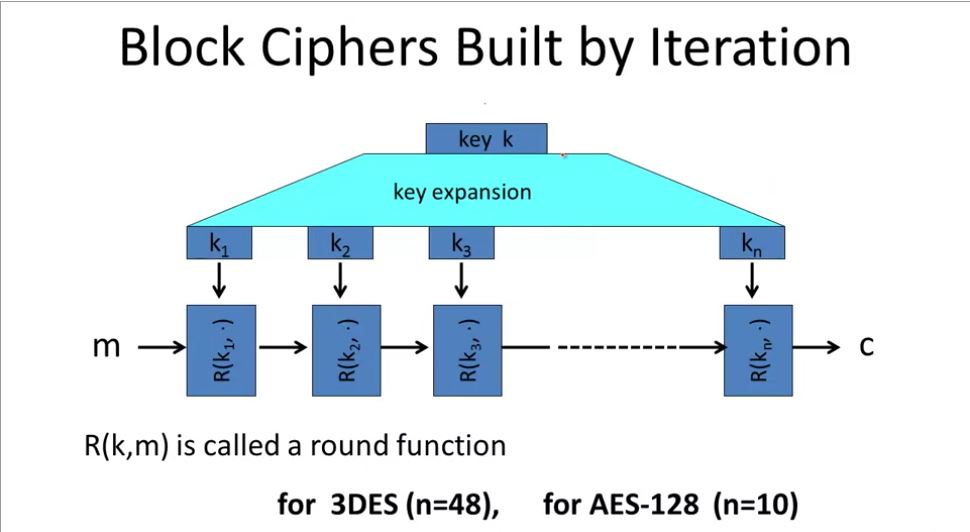
Different ciphers have different amount of rounds. For 3DES it’s 48, and for AES-128 it is 10.

Block ciphers are rather slow compared to stream ciphers. The longer the key, the slower they are. However we can do many things with block ciphers that we couldn’t do with stream ciphers.

Pseudo Random Function (PRF)

A PRF is defined over (K, X, Y) {key-space K, input-space X and output-space Y} with F: K x X -> Y such that there exists an efficient algorithm to evaluate F(k,x).

Note: A PRF doesn’t need to be revertible.

Pseudo Random Permutation (PRP)

A PRP (block cipher) is defined over (K,X) with E: K x X -> X such that: - Exists efficient and deterministic algorithm to evaluate E(k,x) - The function E(k, ・) is one-to-one. - Exists an efficient inversion algorithm D(k,y)

Examples: - 3DES: K x X -> X where X = {0,1}^64 , K = {0,1}^168 - AES: K x X -> X where K = X = {0,1}^128

Any block cipher or PRP is also a PRF : A PRP is a PRF where X = Y and is efficiently invertible.

Secure PRF

Let F: K x X -> Y be a PRF - Funs[X,Y]: the set of all functions from X to Y - S_{F} = { F(k,・) s.t. k ∈ K} ⊆ Funs[X,Y]

Intuition: A PRF is secure if a random function in Fun[X,Y] is indistinguishable from a random function in S_F.

PRF gives us a PRG (PRF => PRG)

Let F: K x {0,1}^n -> {0,1}^n be a secure PRF. Then the following G: K -> {0,1}^{nt} is a secure PRG: G(k) = F(k,0) || F(k,1) || … || F(k,t)

Key property: parallelizable

Security from PRF property: F(k,・) indistinguishable from a random function f(・)

Summary: - Block cipher basically maps n-bits of input to n bit of outputs - Built by Iteration

DES (Data Encryption Standard)

Widely deployed in banking (ACH) and commerce.

DES: Core Idea - Feistel Network

Given functions f_1, …, f_d: {0,1}^n -> {0,1}^n Goal: build invertible function F:{0,1}^{2n} -> {0,1}^{2n}

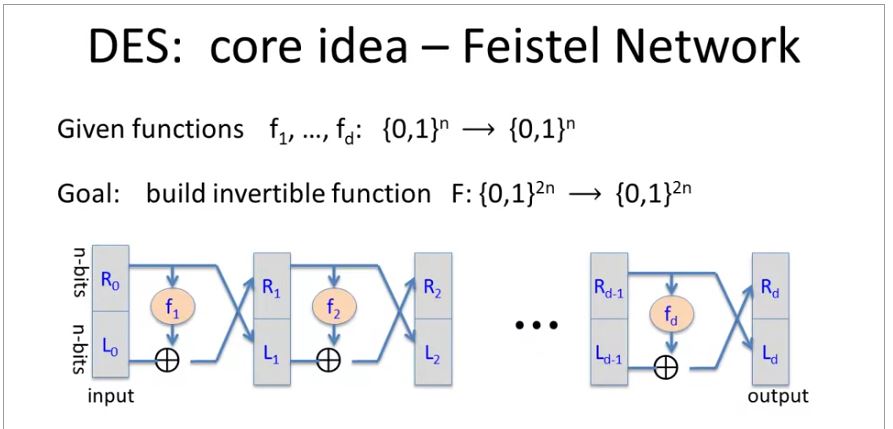
A Feistel Network mapping a 2n bit input to 2n bit output: Encryption Li = R{i-1} R_i = L_i XOR fi (R{i-1}) Decryption Li = f{i+1} (L{i+1}) XOR R{i+1} Ri = L{i+1}

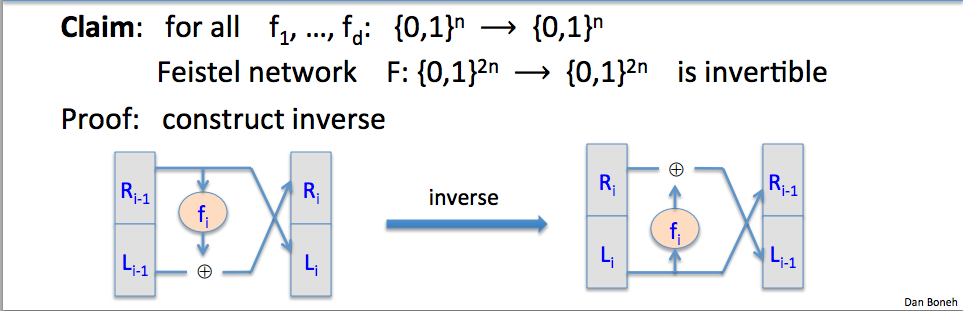
Feistal networks are a general method for building invertible functions (block ciphers) from arbitrary functions. And it’s used in many block ciphers but not AES.

The Luby-Rackoff Theorem proves that if you take a secure PRF and let it go through 3 rounds of a Feistal network, the result is a secure PRP. Formally f: K x {0,1}^n -> {0,1}^n a secure PRF => 3-round Feistel F: K^3 x {0,1}^{2n} -> {0,1}^{2n} is a secure PRP.

DES is a 16 round Feistel network

f_1, … , f_1: {0,1}^32 -> {0,1}^32, f_i (x) = F{k_i, x} where k_i is a round key from the key expansion.

We start with a 64-bit input that gets fed into a Initial Permutation, that mixes the input bits around, this then gets fed into the 16-round Feistel network, which gets fed into Final Permutation that undoes the shuffling around of IP. We are left with a 64-bit output.

For decryption, the algorithm is the same but you use the round keys in reverse-order.

The Function F(k_i, x):

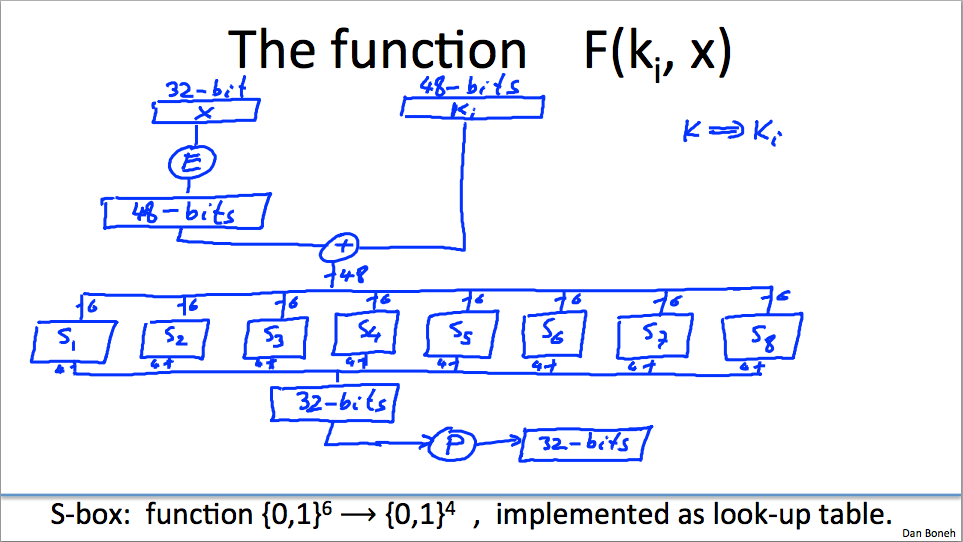
F function

S-boxes

function {0,1}^6 –> {0,1}^4

S-boxes are implemented as lookup tables.

Example: a bad S-box choice - There are good and bad versions of S-boxes. - Mainly we don’t want the S-boxes to be calculated via a linear function, because this would mean that all that DES does is xor’ing and moving bits around. - If DES was wholly linear, this would mean that it’s not fully random. - Choosing the S-boxes at random would not be enough to make them secure, as the chances of them being linear would be too high. The key could be recovered after about 2^24 outputs.

So what are the creators of DES advising to make S boxes lookup tables? - No output bit should be close to a linear function of the input bits - S-boxes are 4 to 1 maps. - …

Exhaustive search on DES

Goal: given a few input/output pairs (m_i, c_i = E(k, m_i)), find key k.

Lemma: Suppose DES is an ideal cipher (2^56 random invertible functions). Then for all m,c there is at most one key k such that c = DES(k,m).

With two input-output pairs, the probability that the key is unique is very close to one for both DES and AES. Hence, two input/output pairs are enough for exhaustive key search.

DES Challenge RSA issued a challenge to break DES exhaustively: - 1997: Internet Distributed Search = 3 months - 1998: EFF machine (deep crack) = 3 days - 1999: combined search = 22 hours - 2006: COPACOBANA (FPGA) = 7 Days (cheap!)

Conclusion of the challenge was ==> 56-bit ciphers should not be used!!

How do we make DES more expensive to do exhaustive search? More rounds!

Method 1: Triple DES.

Triple DES is also 3x slower for encryption :(

The key-size of 3DES is 3*56 bits = 168 bits but does not provide 168 bits security only 118 bits. -> Meet in the middle attack

Why not 2DES For 2DES: exhaustive search is formulated as finding (k_1,k_2) such that E(k_1, E(k_2, M)) = C. A meet-in-the-middle attack is E(k_2, m) = D(k_1,c)

Step 1: Build table of pairs (k0…kN ; E(k0, M)…E(KN, M) Step 2: For all k ∈ {0,1}^56: test if D(k,C) is in 2nd column. Step 3: If found, then E(k^i, M) = D(k,c) => (k^i, k) = (k_2, k1)

Running time = Time = 2* 2^56 * log 2^56 < 2^63 << 2^112

Same attack on 3DES: Time = 2^(118), space = 2^56

Method 2: DESX

E: K x {0,1}^n —> {0,1}^n a block cipher. EX((k,1,k2,k3), m) = k_1 XOR E(k_2, m XOR k_3) key-length = 184 bits. Attack known in 2^120.

Attacks on the implementation of the block ciphers

Side channel attacks

Fault attacks

Conclusion on implementation attacks

Attacks on block ciphers

Linear and differential attacks (Linear cryptanalysis)

Given many input/output pairs, can recover key in less time than exhaustive search (2^56 for DES)

 Pr[m[i_1] XOR … XOR m[i_r] XOR c[j_j] XOR … XOR c[j_v] = k[l_1] XOR … XOR k[l_u] ] = 1/2 + epsilon

For DES, epsilon = 1/(2^(21)) ~= 0.0000000477 because the fifth S-Box is too close to a linear function.

How can we attack it to find key bits?

Given 1/epsilon^2 random (m, c=DES(k, m) ) pairs then

 k[l_1, … , l_u] = MAJ [ m[i_1 , … , i_r] XOR c[j_j, …,j_v] ]

with probability >= 97.7%.

Linear Attacks

Lesson: A tiny bit of linearity in S_5 lead to a 2^42 time attack! NEVER DESIGN YOUR OWN BLOCK CIPHER.

Quantum attacks

If you could build a quantum computer, a generic search problem that would be solved in O( |X| ), can be solved in O( |X|^(1⁄2) ) whatever the function is.

This would cut down the search space: With DES: ~= 2^28, with AES-128 ~= 2^64, which would still be not secure.

Examples: - DES = 2^28 - AES-128 = 2^64 - AES-256 = 2^128

Advanced Encryption Standard (AES) Block Cipher

History

Key sizes = 128, 192, 256 bits.

Larger keys: slower encryption but thought to be more secure.

Block size = 128 bits

Design

AES is a substitution-permutation network. In a Feistal network, half of the bits are not changed in every round. In a subs-perm network, all bits are changed on every round.

AES-128 schematic

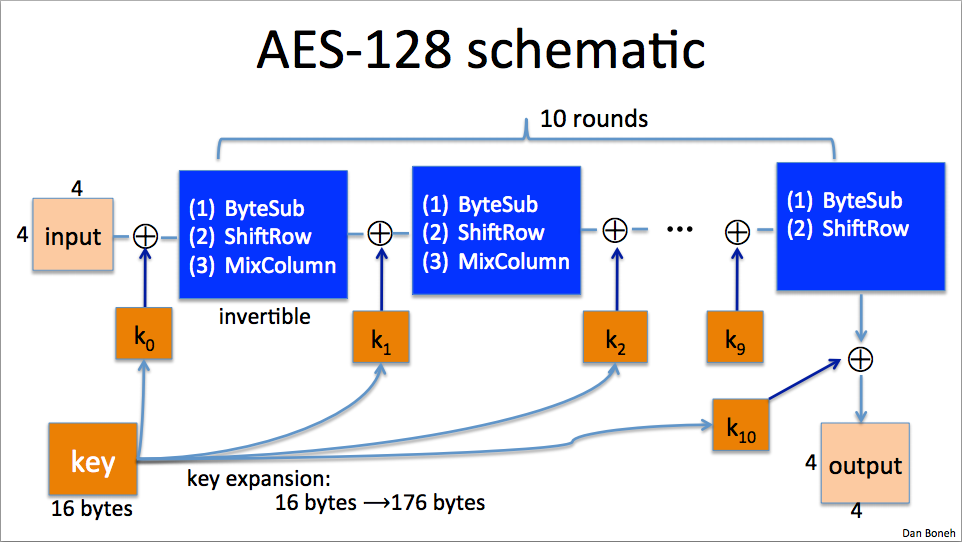
AES-128

AES operates on 128 bits, a 4x4 matrix, each cell containing a byte. Then we XOR with the first round key, apply the round function, x10 and then we get the output. The keys are coming from the 16 bytes AES key using key expansion.

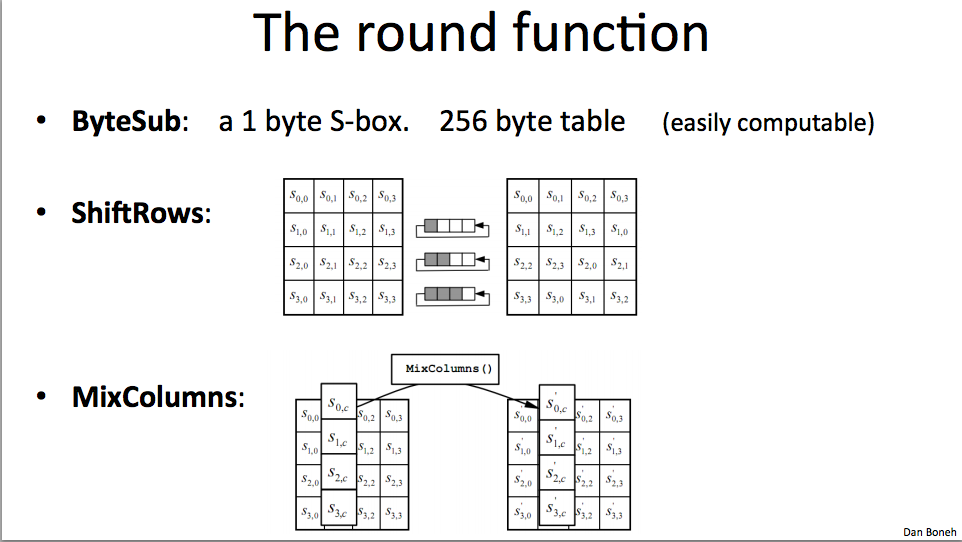
AES-128-RoundFunctions

Overview of the round function: - ByteStub (Byte substitution): one byte S-Box (256 byte table). We take the current cell as an index into the lookup table, and the value is the output. - ShiftRows step: We shift the second row from 1 position, third row by 2 positions and last row by 3 positions. - MixColumns: We apply a linear transformation to each of the communes independently.

How to use AES

If you want to send an implementation over a network. Don’t send precomputed table but algorithm to compute it. And then compute them upon receival.

AES is implemented in hardware (Intel Westmere): + aesenc, aesenclast: one round of AES. + aeskeygenassist: performs AES key expansion. + Claim 14 times faster than OpenSSL on same hardware.

Attacks on AES

Building block ciphers from PRG

Can we build a PRF(block ciphers) from a PRG?

Let’s start with a PRG, G such that G:K -> K^2 be a secure PRG.

Define 1-bit PRF (domain is only 1 bit) F:Kx{0,1} -> K as F(k, x in {0,1}) = G(k)[x]

If G is a secure PRG, then F is a secure PRF on {0,1}^n => Not used in expanded mode due to performance reasons.

Thanks to the Luby-Rackoff theorem, we know that we can thus make a secure PRP with a 3-round Feistal network.

Notes and Review

A block cipher maps n bits of input to n bits of output.

PRF -> function, X -> Y, doesn’t have to be the same. PRP -> One to one revertible function. Domain X=Y. Key concept to build a block cipher.

Any secure PRP is also a secure PRF if |X| is sufficiently large.

Lemma: Let E be a PRP over (K,X) then for any q-query adversary A:

|Adv_{PRF} [A,E] - Adv_{PRF} [A,E] | < q^2 / 2|X|

When X is large, the ratio will be negligible.

So we can say that if E is secure PRP, it is also Secure PRF. From now on, we consider AES or 3DES as secure PRPs.

Share this post on: