Cryptography I - Week 2 - part 2
Feb 5, 2020CryptographyBlock Cipher Share on:
Using Block Ciphers
Modes of operation: One time key
Goal: Build a secure encryption from a secure PRP
The block cipher mode of operation defines the relationships between blocks encoded using the cipher. There are different modes that were created to make it more difficult for an attacker to guess the original content of the message.
Security for one-time key
Let’s start with a threat model (one-time keys) defined as follows: - Adversary’s power: Adv sees only one cipher text - Adversary’s goal: Learn info about PT from CT (semantic security)
Reminder: semantic security for a one-time key. The attacker, if given c_0 and c_1 and m_0 and m1 can’t know which one is the result of what message. Adv{SS} [A, OTP] = | Pr[ EXP(0)=1 ] - Pr[ EXP(1) = 1 ] |
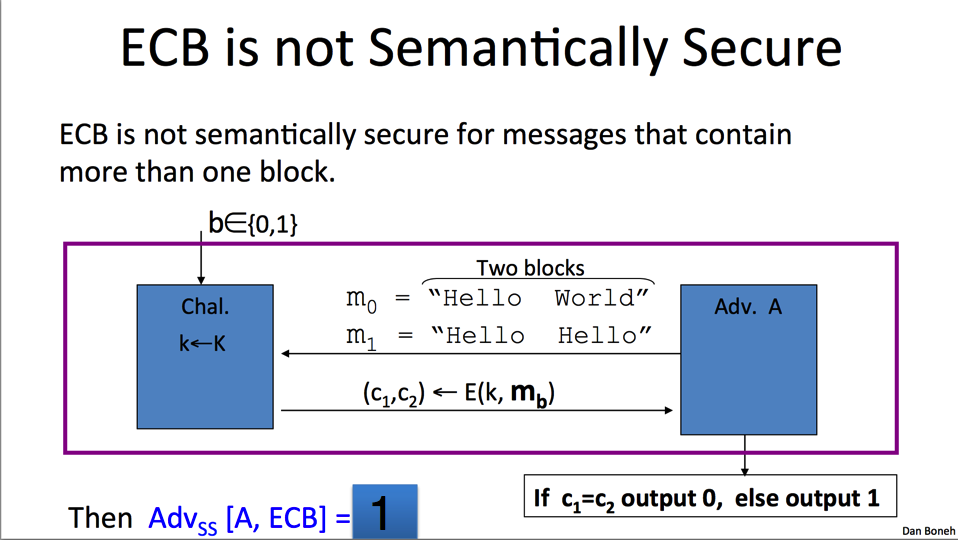
ECB (Electronic Code Book) - One time key
When using ECB, each block of data is encrypted separately and they are then concatenated in the original order. Parallel processing is possible since blocks do not depend on one another. There is no need for an IV. The major problem of ECB is that if the same block of data is encrypted, it will always generate the same ciphertext. This makes it easier for the attacker to guess the original data based on repeating patterns.
ECB is badly broken. It works by breaking down the message into n blocks of size of the block cipher and then encrypt each of the parts individually. Issue, the attacker learns when a two segments have the same value. (if m_1 = m_2 -> c_1 = c_2)
ECB is not semantically secure. ECB is not semantically secure for messages that contain more than one block.
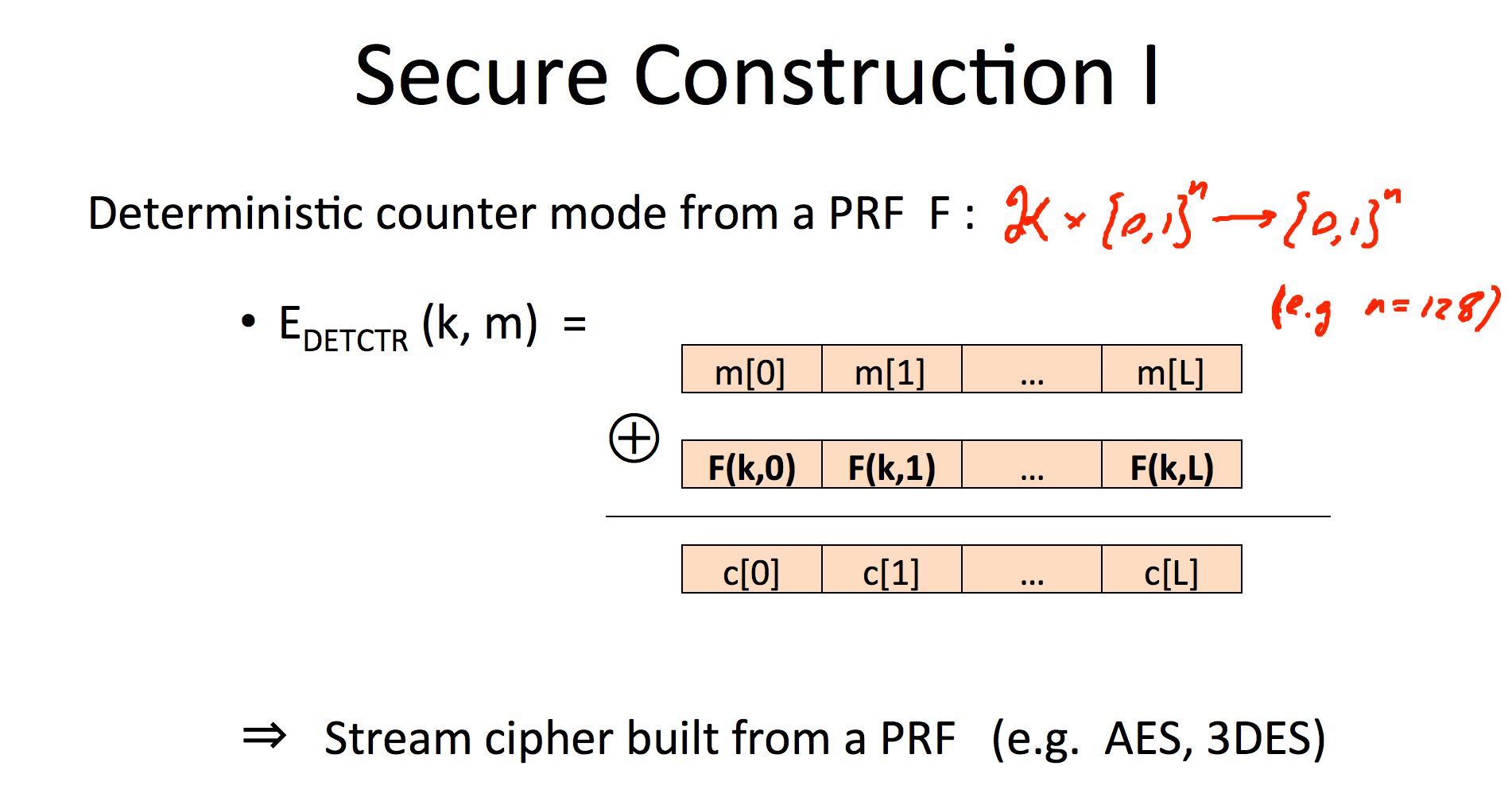
Deterministic counter mode from a PRF F (eg. AES) - One time key
E_{DETCTR} (k,m) = We build a stream cipher from a PRF.
Security for many-time key
Why? Many applications: Filesystems or IPSec, encrypts a lot of traffic with the same key.
When we use a key more than once, the adversary sees many cipher texts with the same key.
Adversary’s power: chosen-plaintext attack, the attacker can obtain the encryption of arbitrary messages of his choice (How does it work IRL? You can email someone, email will be stored encrypted on disk and boom you have m and c).
Adversary goal: Break semantic security
Semantic-security for many-time key is defined exactly as semantic security for a one-time key but he can repeat any of the messages in the challenge that the attacker can choose. ==> Chosen Plaintext attack (CPA).
All the deterministic encryption schemes we’ve seen before are broken under a chosen plaintext attack (CPA).
So how do we fix this?
1) Randomized encryption: - encrypting same message twice gives different cipher text. - Ciphertext must be longer than plaintext. > size(CT) = size (PT) + “#random bits” - Random bits should always be unique in order for it to be semantically secure
2) Nonce-based encryption:
We define a nonce as a value that changes from message to message. The pair (k, n) {k -> key; n -> nonce} should NEVER be used more than once. A nonce should always be unique, it doesn’t need to be random.
We will lool at some examples of chosing a nonce. The nonce can conveniently be a counter (if in-order and reliable transmission channel, no need to transmit nonce). Another method of chosing a nonce could be picking a random nonce. If same key used by multiple machines, the nonce space needs to be very big and picked at random (easier to implement a “stateless” protocol).
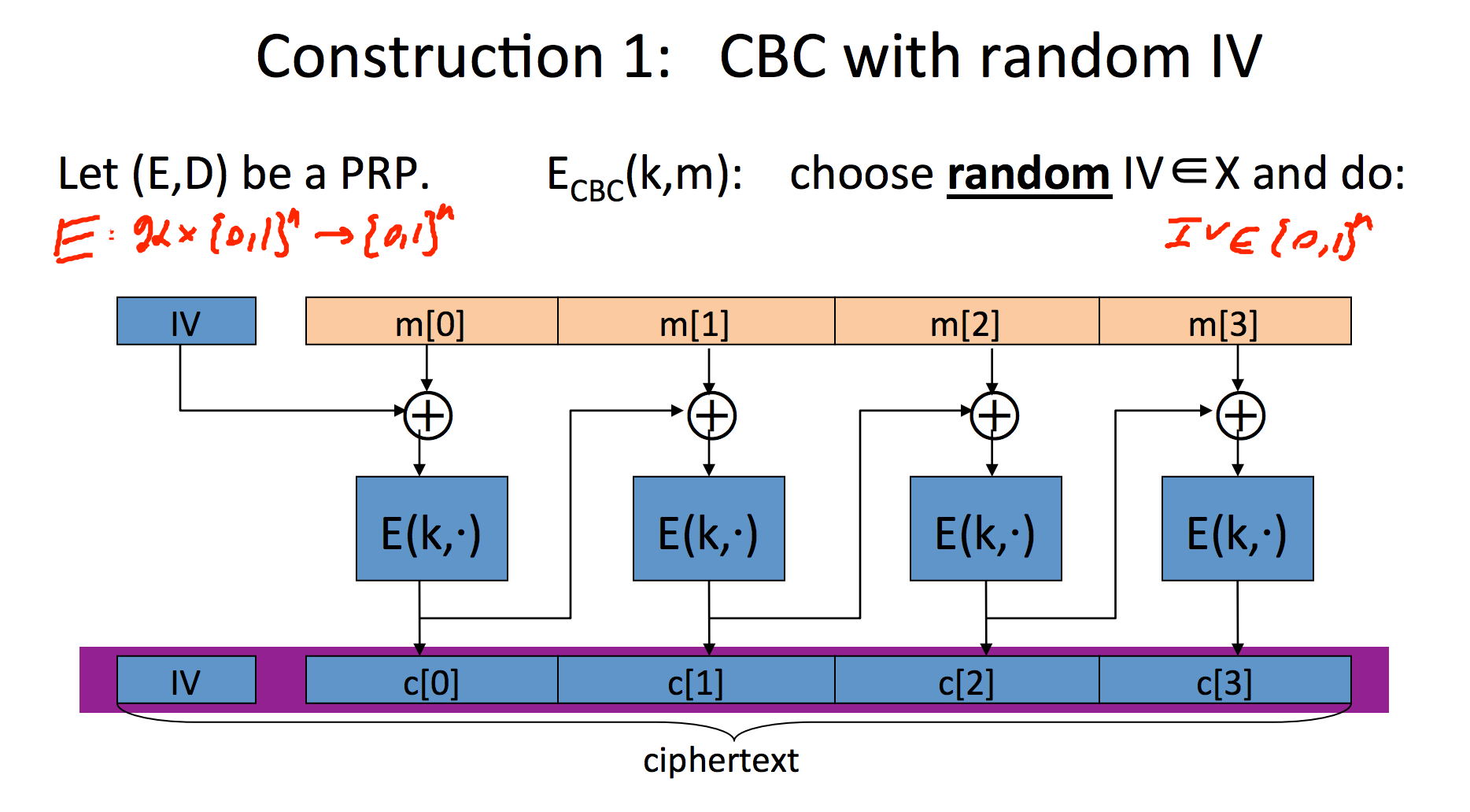
CBC (Cipher Block Chaining with a random IV) - Many time key (CPA security)
IV (Initialization Vector)
An initialization vector is a random (or pseudorandom) fixed-size input used in encryption methods. The main purpose of an IV is starting off an encryption method. In cipher modes like Cipher Block Chaining (CBC) each block is XOR-ed with the previous block. In the first block, there is no previous block to XOR with. An Initialization Vector is used as an input to the first block to start off the process.
If IV is unique for each message, it is called a nonce, which means that it can only be used once. A nonce should be unpredictable. It is also used to prevent attackers from decrypting all messages by guessing the IV. If you use a nonce, the same plaintext may be encrypted using the same key into different ciphertext.
IV-based encryption
When using CBC, each block is XORed with the previous ciphertext before encryption. This eliminates the problem of repeating patterns. An IV is needed to encrypt the first plaintext block. Parallel processing is not possible since the blocks are chained. There is one major disadvantage of CBC: if part of the message is garbled or lost, the remainder of the message is lost.
When we start encrypting the first block, we pick a random IV (initialization vector of length one bloc). We XOR the first message with it before encrypting. IV is publicly known and prepended to the cipher text. Chaining is done by for the next block XORing the cipher text of the first block with the new message and then encrypting.
What security does it provide?
It does provide semantic security:
Adv_CPA [A , E_{CBC} ] =< 2 * Adv_PRP [B, E] + (2 q^2 L^2 / |X| = error term, needs to be negligible)
CBC is secure as long as q^2L^2 << |X| where L is the length of the messages and q is the number of times we used q to encrypt messages.
Applied to AES, this means that after 2^48 blocks, we need to replace the key.
Cipher is not CPA secure if the IV is predictable.
Decryption Circuit for IV based encryption
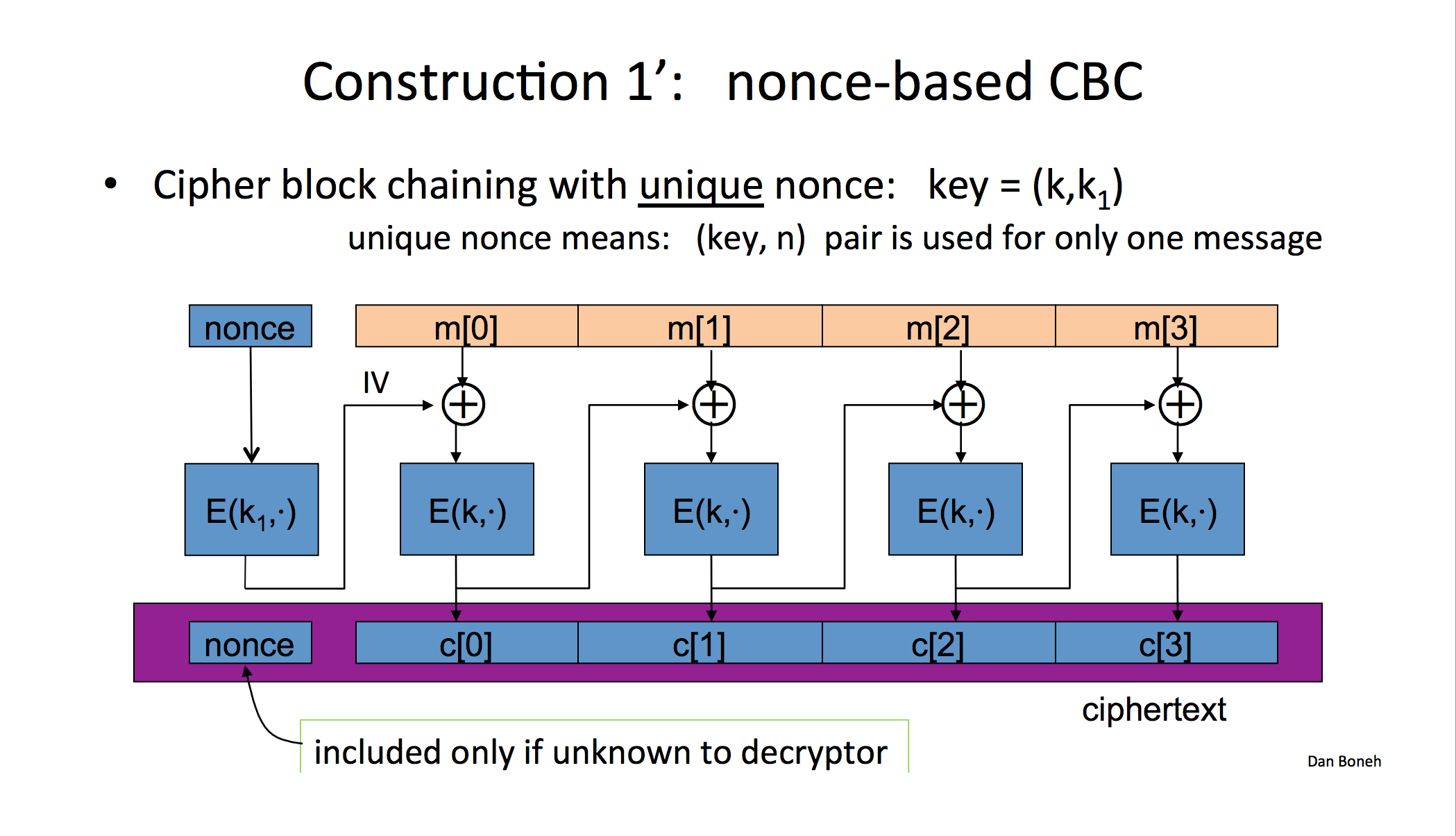
Nonce-based encryption
Cipher-block chaining with unique nonce. (no need to include in first cipher text) : key = (k, k1). > unique nonce means: (key, n) pair is used for only one message.
If nonce is not random, it needs to be xored with first block.
Padding
Block ciphers have a specified fixed length and most of them require that the input data is a multiple of their size. It is common that the last block contains data that does not meet this requirement. In this case, padding (usually random data) is used to bring it to the required block length.
In TLS, you pad the n remaining bytes with the number n. If no pad is needed, add a dummy block.
Randomised Counter-mode (CTR) (superior to CBC)
Unlike CBC, randomised counter-mode doesn’t need a secure block cipher (PRP) but works with a secure PRF because we’re never going to invert the function F.
How does it work?
We pick a random IV, then we XOR the messages blocks with F(k,IV + message block number)
Nonce based counter mode: IV = { 64-bit nonce | 64-bit counter (starts at 0 for every message)}
Note that we can encrypt a maximum of 2^64 blocks per nonce because otherwise the counter overflows and the pad would be used a second time.
We can use counter-mode for more blocks than CBC because the adversary’s advantage is 2q^2L / |X| < CBC’s advantage.
For AES, we can encrypt 2^64 AES blocks with the same key with semantic secrecy.
Advantage: It’s parallelizable! Fast encryption! And is so much better than CBC.
Coparison: CTR vs CBC

